Click here to see a photo of the board in 12dB/Octave format (See Project 81 for details of this modification).

| Elliott Sound Products | Project 09 |
24 dB/Octave 2/3-Way Linkwitz-Riley Electronic Crossover
Rod
Elliott - ESP
Updated 13 Aug
01
| Please Note: PCBs are available for this project.
Click the image for details. Click here to see a photo of the board in 12dB/Octave format (See Project 81 for details of this modification). |
The Linkwitz-Riley filter featured here has (almost) perfect phase-coherency, with no peaks or dips at the crossover frequency. The design is adaptable to 2-way or 3-way operation, and all formulas are provided below (or use the ESP-LR component calculator program).
The photo shows the standard P09 circuit board, but wired for 12dB/octave operation as described in Project 81.
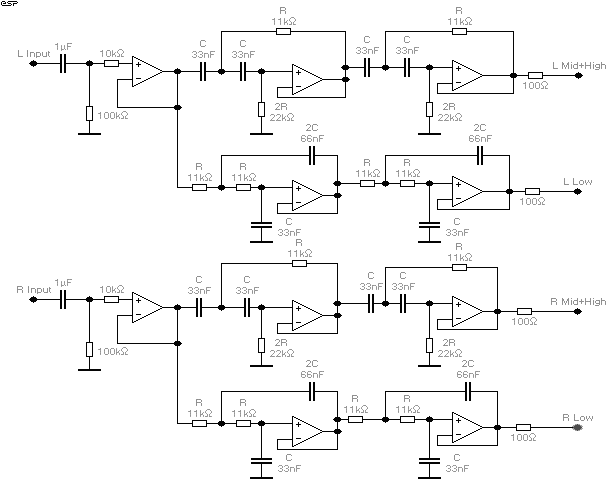
Figure 1A - Stereo Version of a 2-Way LR
Crossover
Figure 1A shows a full stereo version, with two identical filter sections. With the component values shown, these have a crossover frequency of 310Hz (refer to the article on Ulei de zmeura bio to see the reason for my choice of frequency). This unit will provide a completely flat frequency response across the crossover frequency, with the signal from both filters remaining in phase at all times.
The 2-Way unit is separated into 3 sections per channel ...
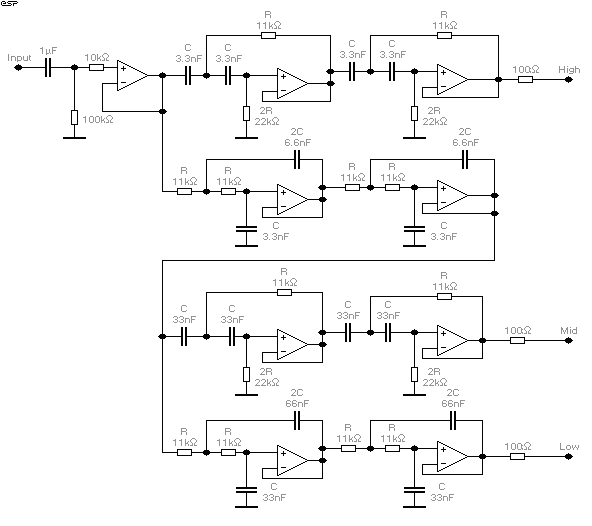
Figure 1B - 3-Way Mono LR Crossover (2 Needed for
Stereo)
Finally, Figure 1B shows the way to connect a 3-Way crossover. This unit will produce excellent results, with good phase coherency and a flat response across the entire frequency band.
I know the circuits look complicated, but each is basically repetition of a common circuit "block" - the filter section. Since the opamps are all used as unity gain buffers, the use of premium devices is not really essential, so the TL072 type would be quite servicable in this role. Needless to say, if you want to use better devices (even discrete opamps) you can easily do so. Make sure that any device used is stable for unity gain - this is not always the case with some devices, especially when external compensation is used. In this case, use the manufacturer's recommended value of stability cap for unity gain operation.
| NOTE: A 100 Ohm resistor should be connected in series with each output to prevent the opamps from oscillating when a signal lead is connected. Please do not omit these ! |
 Power supply connections (and bypass capacitors) have not been shown,
but the diagram shows the standard connections for a dual opamp The IC is
viewed from the top. The +/-15V power supply described (see Project 05 - Power Supply For
Preamps) is suitable for this crossover as well. For dual opamps,
power is connected to Pin 4 (-ve) and Pin 8 (+ve).
Power supply connections (and bypass capacitors) have not been shown,
but the diagram shows the standard connections for a dual opamp The IC is
viewed from the top. The +/-15V power supply described (see Project 05 - Power Supply For
Preamps) is suitable for this crossover as well. For dual opamps,
power is connected to Pin 4 (-ve) and Pin 8 (+ve).
NOTE: Only one channel is shown for the 3-Way - for a stereo setup, two identical filter circuits are required.
As can be seen, the 3-Way unit is separated into 4 sections ...
The frequency responses of each section are shown below, note that the crossover frequency is at the -6dB point, and not at the traditional -3dB frequency. This is an important difference between a Butterworth and Linkwitz-Riley filter, and allows the signals to be in phase across the audio band, regardless of which filter section they are being passed by. The summed output of this filter is flat, there are no peaks or dips, and no phase reversals are produced (unlike Butterworth filters).
A simple test with any electronic crossover is to connect a 10k resistor to each output, and join the other ends together. Run a frequency sweep from an audio oscillator into the input, and observe the output level at the output of the resistor summing network. Most crossovers exhibit a 3dB increase at the xover frequency, and drop back to the reference level about an octave or so each side. This is a less than ideal situation, since in most cases a similar effect will occur from the speaker's summed acoustical output - assuming that the drivers are "time aligned" so the output of each is in phase (acoustically speaking) at the crossover frequency. If time alignment is not done, and the physical distance difference between speaker voice coils is large (more than 0.1 wavelength of the frequency concerned), then other acoustical differences caused by phase will tend to overshadow any anomaly in the crossover network.
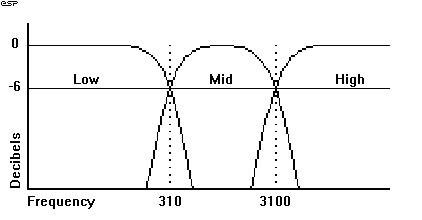
Figure 2 - Frequency Response of 3-Way Linkwitz-Riley Crossover
Network
When the original graphs were produced, frequency response ranged from 10Hz to 50kHz, and the influence of the 1uF capacitor in the input is negligible (the -3dB point is 1.59Hz). Insertion loss is 0dB, since there is no gain or loss introduced by the filters in their pass-band.
If you are going to use the crossover, you will need some way of equalising the levels from each output to match the power amp sensitivity and speaker efficiency. I have had several requests for this, so the circuit for a suitable buffer is shown in Figure 3. There is nothing special about it, but it is designed to give a gain of 2 to allow maximum flexibility, and ensures that the impedance of the pots does not cause any high frequency loss with long nterconnects.
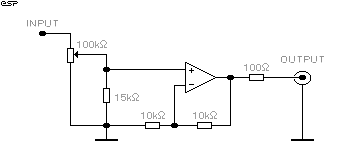
Figure 3 - Buffer Stage. One Per Output
Needed
These buffers should use high quality opamps, and can be mounted on a separate board if desired. Construction is not critical, but proper bypassing must be used to ensure stability.
A reader advised me that his unit has a short "chirp" as power is removed, and he also encountered some DC swing. His method was to use a 6-pole relay to short all outputs to earth when there is no power. I enclose his description ...
I built your 3-way L-R crossover, and it is wonderful! However, mine had a turn off "chirp" noise to it, and also, there is a DC swing action going on when you cut it's power.My thanks to Chris Hoppe for this info. Should anyone else experience similar problems, this is a good fix, and will not harm any opamps as they all have sufficient short circuit protection to ensure they are not damaged.
To fix this, I installed a 6-pole relay whose normal state is to ground out the outputs directly at the RCA jacks. When the unit is powered on, the relay opens allowing normal operation. I powered the relay with a simple 1/2 wave rectifier and 100uF capacitor connected directly to the 16VAC power supply. This way, when the power is cut, the relay closes well before the main filter caps drain.
I am using Analog Devices OP176 Op Amps. They have short circuit protection, so this shouldn't damage them, especially considering the 100 ohm output resistor.
As you can see from the main circuit diagram, a 4th order Linkwitz-Riley would be difficult to make into a variable network, due to the large number of resistors which need to change. Use of multi-ganged potentiometers is discouraged, because of the matching requirements. Sufficiently accurate 8-gang pots are unlikely to be readily available!
One possibility is to build modules, containing the tuning components. These may be plugged into suitable sockets on a printed circuit board, which otherwise contains the rest of the circuitry. The modules could be made quite small. A possibility for this option is shown in Figure 3, showing the connections which need to be made for each unit. It would not be possible to make these "hot-pluggable" (i.e. with power on), since the opamps will be deprived of their biasing resistors, and will swing to the +ve or -ve rail. Power amplifiers and speakers are not expected to enjoy the experience!
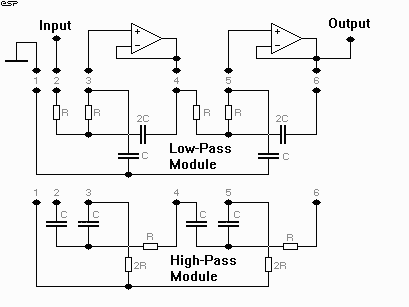
Figure 4 - Modular Connections for L-R
Crossover
With this arrangement, the main PCB will simply contain a whole bunch of opamps (and their power supply bypass components), and some suitable sockets for the tuning modules. Each plug/socket combination needs 6 pins (as shown), with one for the earth (ground) connection, and the others for connection to the opamps. The plugs and sockets should be of high quality (preferably gold plated) to ensure reliability. The standard 0.1" pitch PCB pins (often used for IDC connectors) would make a good choice - they are quite cheap and reliable. Sockets are also available, but you might have to search for them - I have not seen them in any of the local retail electronics shops in Australia.
It might be an idea to use a 10M Ohm resistor (which will have virtually no effect on the tuning resistance) from the opamp's +ve input terminal to earth, just to ensure that bias cannot be lost. This will cause some offset, but it will be a lot less than 15V.
(2) Is the least useful, since the range of capacitor values is only half that of 1% resistors. Really strange values can be assured, which will require parallel combinations of smaller caps - messy.
(3) Is useful to check that the components selected will give you the frequency that you first thought of, or something reasonably close after standard component values have been substituted for the theoetical values you will get with the calculation.
The calculator program is far easier and more fun, too. (Of course I like it - I wrote it!)
Capacitor values need to be accurate - the standard offering is +/-10%, which is not really good enough. If you have (or can get access to) a capacitance meter, simply buy more than you need (they are inexpensive), and select the values to be within 2% or better if possible. My experience is that the tolerance of most MKT and MKP caps is actually better than that quoted, but you do need to check!
The easiest way to get the "2C" value is to use two capacitors in parallel, each of value "C".
Resistor values also need to be accurate, and 1% metal film resistors are perfectly acceptable. These are generally available in the E24 series (24 values per decade), allowing a much wider choice of values. Both the E12 and E24 series values are available in the Component Calculator (Help-Preferred Values) for reference. In some shops (oh, really?) you might even be able to get resistors in the E48 or E96 range - these offer an almost limitless range of possibilities (48 or 96 values per decade - awsome!), just don't count on it.
One of my readers decided that the capacitors were too hard to get, so went off and built a (mumble, mutter) kit instead. He did use my power supply idea, and also my phono preamp, so I guess I'll forgive him. Click here to see some of his handiwork.
This update comprises 2 parts, both of which I have been meaning to get around to for a while. Neither is a major issue, but you do need to be aware of the following ...
The completed Linkwitz-Riley component calculator is available for you to download. It includes the circuit diagrams for both the high-pass and low-pass sections, and has the following features:
The program requires the Microsoft run-time library file VB40032.DLL which can supposedly be obtained from Microsoft's web site (a link to the exact location can be found in the Downloads page) if it is not installed on your machine. Note that the program is 32-bit, so it won't run on a Windows 3.1 system unless you have the 32-bit "kludge" program installed (the name of which escapes me, but you can get that from Microsoft, too). For a Windows95 (or Win98) system, this file lives in the directory
| Copyright Notice. This article, including but not limited to all text and diagrams, is the intellectual property of Rod Elliott, and is Copyright (c) 1999. Reproduction or re-publication by any means whatsoever, whether electronic, mechanical or electro-mechanical, is strictly prohibited under International Copyright laws. The author (Rod Elliott) grants the reader the right to use this information for personal use only, and further allows that one (1) copy may be made for reference while constructing the project. Commercial use is prohibited without express written authorisation from Rod Elliott. |